Le théorème de quantité de mouvement (de Froude) renseigne sur la force de propulsion (ou de traction) d'une hélice, mais ne donne pas de détails sur son design; autrement dit, cette méthode globale ne tient pas compte des caractéristiques géométriques et aérodynamiques de la section de la pale (ou du profil). Toutefois, on peut prendre en compte les forces qui agissent sur un élément de la pale et les intégrer sur le rayon de l'hélice pour prédire la traction et le couple de l'hélice grace à la THÉORIE DE L'ÉLÉMENT DE PALE : La théorie de l'élément de la pale permettra cette fois-ci de visualiser les composantes de la vitesse induite introduite dans la méthode de froude et d'établir des relations géométriques importantes entre les différents vecteurs vitesses influençant l'écoulement abordant un élément de la pale. Cette théorie nous faira connaître le couple absorbé par un éIérnent de la pale et la poussée générée par cet élément de pale. Puisque cette théorie n'étudie qu'un élément de la pale, les éléments pourront être sommés pour obtenir la poussée totale associée au couple absorbé par l' hélice.

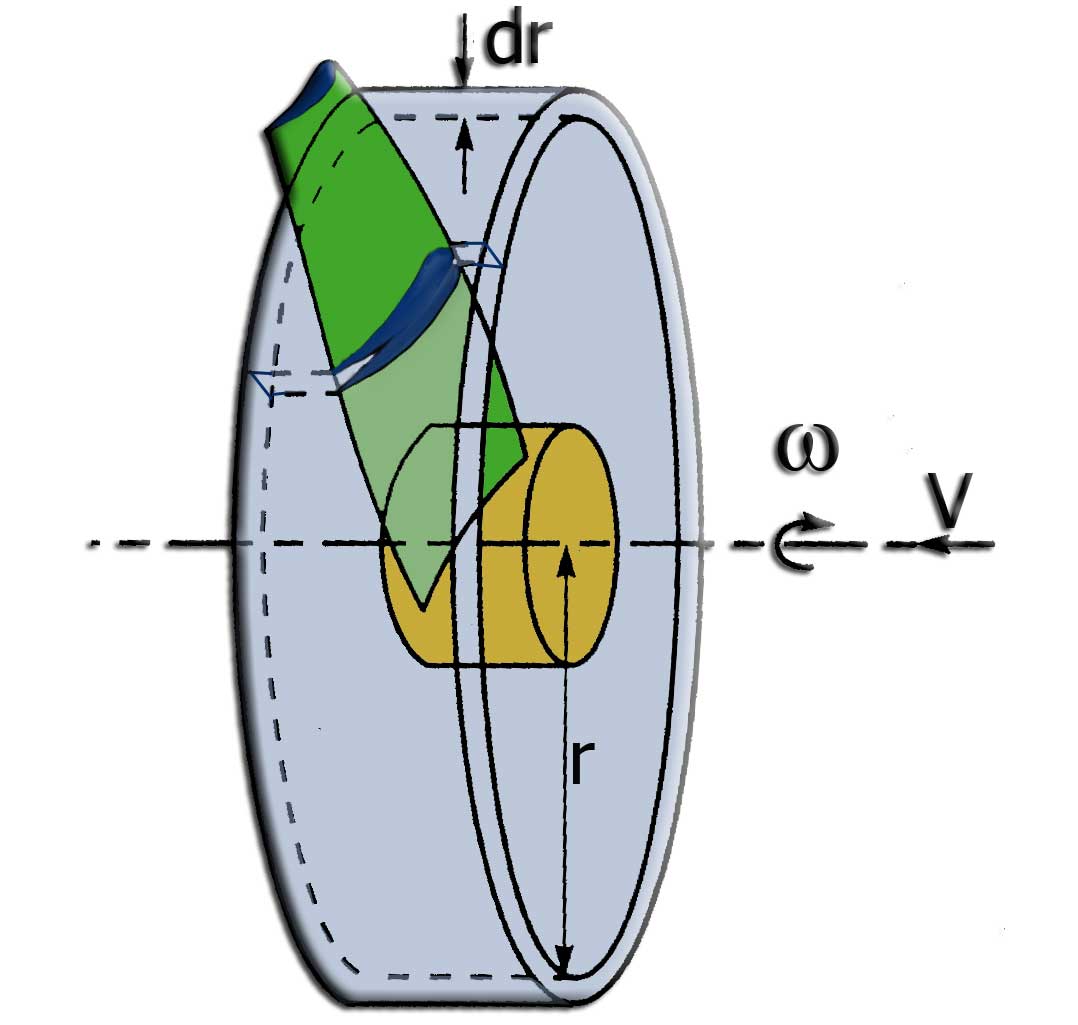
figure 1

La figure1 montre un rotor tournant à vitesse angulaire (a) avançant à une
vitesse V dans l'air Une vue de coupe d'un élément d'une pale de largeur dr situé à une
distance r de l'axe du rotor est représentée à la figure 2

 

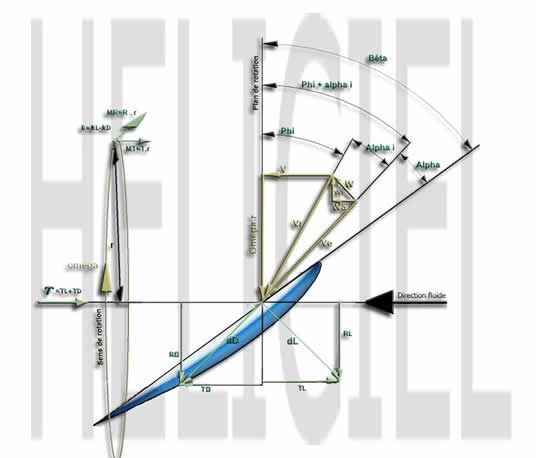
figure2

La figure illustre le fait qu'un élément de la pale n'est pas sujet à un écoulement ayant une vitesse résultante au profil qui dépend uniquement de la vitesse de déplacement du rotor et de sa vitesse de rotation (Vr = V+ wr) , mais bien d'une vitesse d'entrée au profil Ve influencée par les vitesses induites tangentielles wt et axiales wa par le rotor. À l'aide de simples relations de sommes de forces sur les axes suivant le plan de rotation et de l'axe de rotation du rotor, il est possible d'établir les équations de poussée et de couple absorbé par un élément de largeur dr d'une pale :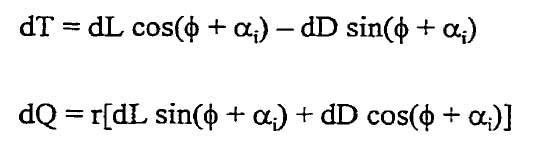

   

equ. 1 et 2

Dans ces équations, dL et dD sont les éléments de forces agissant sur le profil et peuvent être calculés à l'aide du coefficient de portance (CL ou Cz ), du coefficient de traînée (Cd ou Cx) et de la corde (c) du profil au rayon local (r) de Ia pale, pour un anneau de largeur dr (delta de rayon entre deux elements annulaires)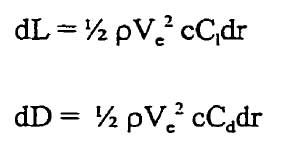

equ.3 et 4

l'équation de poussée dT de l'élément de la pale est utilisée pour évaluer la poussée développée par un anneau circulaire de rayon r et de largeur dr ayant un nombre de pales B. Combinant les équations 3 et 4 à l'équation 1, la poussée sur l'anneau circulaire donne :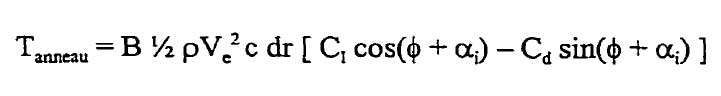

la poussée générée par l'anneau est :

 

En combinant ces deux équations en égalant les poussées générées par les anneaux,
I'équation suivante peut être développée :

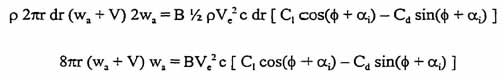
equ 6 et 7

Avec:

L'équation 7 est la première d'un système de deux équations à deux inconnues ayant comme inconnues wa et wt, utilisé pour résoudre les vitesses induites par la pale du rotor...

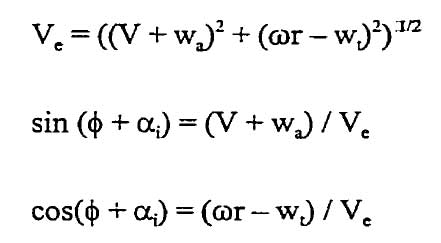
Extrait du mémoire de mr Joncas

References bibliographique helice